
What is PROC Transpose in SAS?
In clinical programming and data analysis, datasets often come in a variety of structures that don’t always align with the needs of analysis or reporting. For example, you may receive data in a "long" format where each observation (row) represents a single event or time point for a subject, but your analysis requires the data in a "wide" format where each subject has a single row with multiple variables representing different time points or conditions.
In SAS, one of the most efficient ways to restructure your data is by using the PROC TRANSPOSE procedure. PROC TRANSPOSE allows you to convert data from rows to columns and vice versa quickly and easily, without having to manually manipulate the dataset. This procedure is especially useful when preparing datasets for clinical trial reporting, where you need to generate summary statistics or cross-tabulations that require data in a specific format.
PROC TRANSPOSE Syntax
This section explains the essential and optional syntax of PROC TRANSPOSE, outlining how it can be applied to restructure datasets in SAS. By specifying the appropriate options, PROC TRANSPOSE allows for flexible data transformation. Here’s the general syntax:
proc transpose data=<input-dataset> out=<output-dataset>;
by <grouping-variables>;
id <identifier-variable>;
var <variables-to-transpose>;
run;
Key Components of the Syntax:
- data=: Specifies the input dataset to be transposed.
- out=: Defines the name of the output dataset that will contain the transposed data.
- by: Lists the variables by which the data will be grouped before transposing. This means that the data will be transposed within each group defined by these variables.
- id: Indicates the variable whose unique values will become the column headers in the transposed dataset.
- var: Specifies the variables whose values will be transposed into the new columns.
In addition to these key components, PROC TRANSPOSE also offers several optional arguments that provide greater control over the process, allowing users to customize the output as needed.
PROC TRANSPOSE offers several optional arguments that provide greater control over the transposition process. Some of the more frequently used optional arguments include:
- DELIMITER=: Allows users to define a character that will separate components in the names of the transposed variables in the resulting dataset.
- LABEL=: Allows you to assign a custom name for the variable that contains the label of the variable being transposed.
- PREFIX=: Specifies a prefix for the names of the transposed variables in the output dataset.
- SUFFIX=: Specifies a suffix to append to the names of the transposed variables.
A comprehensive list of all optional arguments and their functionalities can be found in the SAS documentation (PROC TRANSPOSE documentation).
PROC TRANSPOSE Example: Restructuring Data in SAS
The code below will create a dataset showing the number of hours worked by each employee. The structure of the original dataset, workweek, is one record per employee per day.
data workweek;
input ID Employee $ Day $ 13-21 Hours;
datalines; 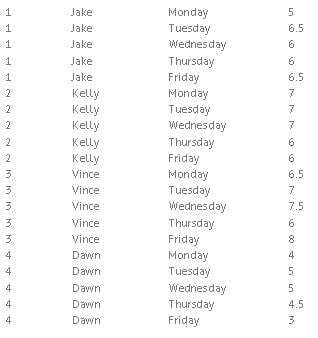
;
run;
In this dataset, the goal is to restructure the data so that each employee has a single record, with separate variables for each day of the week. This transformation can be accomplished using the PROC TRANSPOSE procedure as follows:
proc transpose data=workweek out=workweek2(drop=_name_);
by id employee;
var hours;
id day;
run;
This could also be achieved by using an array:
Here is the dataset created by the PROC TRANSPOSE:

Handling Multiple Variables with PROC TRANSPOSE
PROC TRANSPOSE in SAS is not only capable of restructuring a single variable but also allows users to handle multiple variables simultaneously. This feature is particularly useful in clinical data analysis, where multiple measurements for different parameters need to be organised into a more compact format.
To transpose multiple variables, the VAR statement can include a list of variables that you want to transform into new columns. When using this approach, each variable specified will have its own set of transposed columns in the output dataset.
Consider a dataset that records the scores of students across different subjects for various assessment periods. The initial dataset, scores, is structured as follows:
data scores;
input StudentID $ Subject $ Assessment1 Assessment2
datalines;
S1 Math 85 88
S1 Science 90 92
S2 Math 78 80
S2 Science 83 85;
run;

In this dataset, each student has scores for two assessments in different subjects. To restructure this dataset such that each student has a single record with scores for each subject and assessment, PROC TRANSPOSE can be employed as shown below:
proc transpose data=scores out=transposed_scores(drop=_name_);
by StudentID;
var Assessment1 Assessment2;
id Subject;
run;

In this example:
The BY statement groups the data by StudentID.
The VAR statement lists Assessment1 and Assessment2 as the variables to be transposed.
The ID statement indicates that the values of the Subject variable will become the new column headers in the transposed_scores dataset.
The resulting dataset has columns for StudentID, Math and Science.
This flexibility in handling multiple variables allows researchers and analysts to tailor their datasets to better meet the requirements of their analyses and reporting needs. PROC TRANSPOSE simplifies the data restructuring process, enabling efficient data management and analysis in SAS.
Thought Experiment: Transposing Data Using PROC SQL
Although PROC SQL is not designed for data transposition, it is technically possible, though highly inefficient, to achieve with extensive coding. Attempting this exercise highlights important programming concepts, such as tree traversal, which are fundamental to data structuring and file searching in SAS. While PROC SQL can transpose data in limited cases, the method quickly becomes impractical as complexity grows. PROC TRANSPOSE remains the recommended and scalable tool for reshaping datasets.
Example Data:

Wide-to-Long
This step reshapes data by converting it from a wide format to a long format using PROC SQL. Each variable is selected, renamed, and combined with UNION to form a new column. This can be done dynamically through macros to handle multiple variables.

Long-to-Wide
The second step transforms the long format back to wide. By using CASE WHEN with aggregation functions like MAX, new columns are created for combinations of ID variables. This approach becomes complex when multiple ID variables and distinct values are involved, requiring tree traversal techniques.
Tree Traversal
Tree traversal involves navigating through a tree-like structure, starting at the root and reaching the leaves. It can be done using Depth-First Search (DFS), where we go down to the leaf first before exploring other branches. There are two main types of DFS: pre-order (visit node before children) and post-order (visit node after children). This method helps process each node efficiently, especially when working with data structures like variables in SAS. The traversal method selected depends on the task at hand.

The Solution
To implement the transposition in SAS, we treat the dataset as a tree structure with BY, ID, and VAR variables. We use macros to loop through different ID values and generate columns for each combination. This is done using nested %DO loops, which mimic the tree traversal process. For multiple ID variables, recursion is used to create more complex loops. The process works by identifying child nodes (ID combinations), and the algorithm traverses down the tree before reaching the leaf nodes. Recursion enables deeper iteration and more flexibility in generating the transposed dataset.
Tree traversal and recursion provide greater flexibility in handling complex transpositions with multiple ID variables, but this increased flexibility comes at the cost of both complexity and efficiency. These techniques require more intricate coding and processing time compared to the straightforward approach offered by PROC TRANSPOSE.
Conclusion
PROC TRANSPOSE is a highly efficient and user-friendly tool for reshaping data in SAS, especially when converting datasets from long to wide format. It requires fewer lines of code, is quick to implement, and can automatically handle both numeric and character data types, making it versatile for a range of tasks. Its simplicity and speed make it an ideal choice for clinical programmers working with large datasets that need restructuring.
However, the procedure does have some limitations, particularly around controlling variable names, as it often defaults to generic names like COL1, COL2, unless customized with options like PREFIX=. It also requires clean, well-structured data to function smoothly. Despite these challenges, PROC TRANSPOSE remains an excellent option when your primary goal is to efficiently reshape data with minimal effort.
Request a Consultation


